Pembiasan Cahaya

Pembiasan cahaya terjadi akibat pembelokan cahaya ketika melewati dua medium yang berbeda kerapatannya. Pada kasus pensil yang terlihat patah, cahaya dibelokkan ketika masuk dari udara ke air. Air memiliki kerapatan yang lebih besar daripada udara. Perbedaan kerapatan inilah yang menyebabkan terjadinya pembiasan cahaya. Contoh pembiasan cahaya dalam kehidupan sehari-hari, misalnya (Agus Krisno, 2008: 293):

a)      Batu yang berada di dasar bak mandi tampak lebih dangkal.

b)      Bintang-bintang di langit tampak berkedap-kedip.

c)      Uang logam yang ada di di dalam air tampak lebih besar.

Hukum Pembiasan

Terjadinya pembiasan dibuktikan oleh seorang ahli matematika dan perbintangan Belada pada tahun 1621 bernama Willebrord Snell. Kesimpulan percobaannya dirumuskan dan dikenal dengan Hukum Snellius. Hukum Snellius menyatakan sebagai berikut (Sears dan Zemansky, 2001: 499):

a)      Sinar datang, sinar bias, dan garis normal terletak pada satu bidang datar.

Perbandingan antara proyeksi sinar datang dan proyeksi sinar bias pada bidang batas merupakan bilangan tetap yang disebut indeks bias.

Hukum Snellius tentang pembiasan

Indeks Bias Suatu Medium

Kerapatan suatu medium dinyatakan dengan indeks bias medium tersebut. Indeks bias (n) berkaitan dengan cepat rambat dan panjang gelombang cahaya ketika melewati medium. Hubungan cepat rambat cahaya dan indeks bias dikemukakan oleh Christian Huygens (1629-1695) dengan persamaan (Murtono, 2008: 2): 

n = c/v

Keterangan:

n  =  indeks bias mutlak

c  = laju cahaya di udara (m/s)

v  = laju cahaya dalam medium (m/s)

Persamaan ini menyatakan bahwa indeks bias suatu medium adalah perbandingan cepat rambat cahaya di udara dengan cepat rambat cahaya pada medium yang bersangkutan. Cahaya merupakan gelombang sehingga mempunyai frekuensi dan panjang gelombang. Jika persamaan v = λf pada gelombang disubstitusikan pada persamaan, maka menjadi (Tim Abdi Guru, 2006: 225):

n = (λ₁f₁)/ (λ₂f₂)

karena frekuensi cahaya tetap, maka f₁ = f₂ dan persamaan menjadi:

n = λ₁/λ₂

Keterangan:

n  = indeks bias medium

λ₁  = panjang gelombang cahaya di udara (m)

λ₂  = panjang gelombang cahaya dalam medium (m)

 

Pemantulan Sempurna

Perhatikan berikut!

Ketika sudut datang terus di perbesar, suatu saat akan sampai pada kondisi dimana sudut pantul  sama dengan 90^o atau berada pada bidang pertemuan kedua medium. Pada kondisi ini besar sudut i disebut juga sudut kritis. Kemudian jika kamu perbesar kembali sudut datang dari cahaya melebihi sudut kritis, pada saat inilah pemantulan sempurna mulai terjadi (Tim Abdi Guru, 2006: 227).

Dari penjelasan di atas, maka dapat diambil kesimpulan bahwa pemantulan sempurna terjadi apabila:

a. Sinar datang dari medium yang lebih rapat ke medium yang renggang. Sudut datang melebihi sudut kritis. b. Sudut kritis adalah sudut datang yang sudut biasnya 90^o, atau sinar yang dibiaskan pada bidang batas.

Pembiasan Cahaya pada Lensa Cekung

a. Bagian-bagian Lensa Cekung

Keterangan gambar:

SU                         = sumbu utama

O                           = titik pusat optik lensa

F₁ dan F₂              = titik api (fokus) lensa

O - F₁ dan O - F₂  = jarak titik api lensa

R₁ dan R₂                  = jari-jari kelengkungan lensa

P₁ dan P₂                  = titik pusat kelengkungan lensa

(I), (II), (III)         = nomor ruang untuk meletakan bayangan

(I), (II), (III), (IV)= nomor ruang untuk meletakkan benda

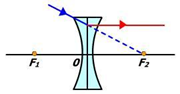
Sinar Istimewa Lensa Cekung

Sinar-sinar istimewa pada lensa cekung adalah sebagai berikut (Agus Krisno, 2008: 295):

1. Sinar yang datang sejajar sumbu utama dibiaskan seolah-olah dari titik fokus F_1.

 2. Sinar yang datang seolah-olah menuju ke titik fokus F₂ dibiaskan sejajar sumbu utama

3. Sinar yang datang melalui titik pusat optik akan diteruskan.

Lukisan Bayangan Lensa Cekung

Melukis bayangan pada lensa cekung dilakukan dengan menggunakan sinar-sinar istimewa pada lensa cekung. Posisi benda sama-sama berada di ruang IV di depan lensa sehingga bayangan yang terjadi selalu maya, diperkecil, sama tegak dan berada di ruang I seperti gambar berikut:

Rumus Lensa Cekung

Lensa cekung menyebarkan sinar sehingga disebut lensa negatif. Nilai jarak fokus (f) dan jari-jari kelengkungan lensa (R) selalu negatif. Adapun persamaan rumus lensa cekung sama dengan persamaan pada cermin cekung dan cermin cembung (Tim Abdi Guru, 2006: 231).

Pembiasan Cahaya pada Lensa Cembung

Lensa cembung atau lensa konveks merupakan lensa yang bersifat mengumpulkan cahaya sehingga disebut sebagai lensa konvergen. Berkas cahaya sejajar yang dikenakan pada salah satu sisi lensa cembung akan dibiaskan mengumpul di satu titik yaitu di titik fokus lensa. Bentuk lensa cembung ada tiga macam, yaitu cembung rangkap (bikonveks), cembung datar (plan konveks), dan cembung-cekung (konkaf konveks) (Sumarwan, 2010: 284).

Bagian-Bagian Lensa Cembung

Keterangan gambar:

SU                     = sumbu utama

O                       = titik pusat optik lensa

F₁ dan F₂          = titik api (fokus) lensa

O–F₁ dan O–F₂                = jarak titik api lensa

P₁ dan P₂              = titik pusat kelengkungan lensa

R₁ dan R₂          = jari-jari kelengkungan lensa

I, II, III                         = nomor ruang untuk meletakkan benda
I, II, III, IV      = nomor ruang untuk bayangan benda

Sinar Istimewa Lensa Cembung

Sinar-sinar istimewa pada lensa cembung juga ada tiga macam. Sinar-sinar ini digunakan untuk membentuk bayangan ketika sebuah benda diletakkan di depan lensa cembung. Sinar-sinar istimewa pada lensa cembung tersebut adalah:

1. Sinar yang datang sejajar sumbu utama dibiaskan melalui titik fokus F2.

2. Sinar yang datang melalui titik fokus F₁ dibiaskan sejajar sumbu utama.

4. Sinar yang datang melalui titik pusat optik akan diteruskan.

Lukisan Bayangan Lensa Cembung

Sama halnya seperti ketika kamu melukis bayangan pada cermin dan lensa cekung, maka ketika melukis bayangan pada lensa cembung pun cukup menggunakan dua sinar istimewa. Bayangan yang terjadi merupakan hasil perpotongan sinar-sinar bias atau perpanjangan sinar-sinar bias (Saiful Karim, 2008: 299).

Rumus Lensa Cembung

Lensa cembung disebut lensa positif karena nilai jarak fokus dan jari-jari kelengkungannya selalu positif. Hubungan antara jarak benda (s), jarak bayangan (s’), dan jarak fokus (f) pada lensa cembung sama dengan persamaan pada cermin cekung, cermin cembung, dan lensa cekung.

Kekuatan lensa menyatakan kebalikan dari nilai jarak fokus lensa. Satuan jarak fokus lensa untuk perhitungan kekuatan lensa harus dinyatakan dalam meter. Kekuatan lensa dirumuskan

P = 1/f

Keterangan:

P           = kekuatan lensa atau daya lensa (dioptri)

f             = jarak fokus lensa (m)

Pembiasan Cahaya 2016-04-09T07:31:00-07:00 Rating: 4.5 Diposkan Oleh: Mantan Tentor Fisika